离散数学-期末复习
Published:
离散数学课程期末复习
数结构
代数系统
二元(一元)运算-Binary(Unary) Operation
定义
S is a set, a function f: S×S→S is called a binary operation over S-S上的二元运算
特性
唯一性(Uniqueness)
封闭性(Existence)任意两个元素的运算结果都属于S
性质
交换律-commutative operation 可交换的
结合律-associative operation 可结合的
幂等律-idempotent operation x*x = x
/S中满足x·x =x的x被称为运算·的幂等元/
分配律-distributive operation 可分配的
吸收律-absorption law
x *(x·y)=x
x ·(x*y)= x
消去律-cancellation law
if x · y = x · z,and x != 0, then y = z
特异元素
单位元(幺元)-identity element(感觉有点儿像乘法里的1)
*is a binary operation over A, if there exists el(or er)∈ A, such that for any x belongs to A,
el * x=x(or x * er =x)
then el(er)is a left (right) identity element of A.
定理:如果el,er分别为左右单位元,el=er=e
proof: el=el*er=er
推论:单位元是唯一的
proof: let e’ be the other indentity element.
e’=e*e’=e
零元-zero element(乘法中的0)
*is a binary relation over A, if there exists 0l(or 0r)∈ A,such that for any x belongs to A,
0l * x= 0l(or x * 0r= 0r)
then 0l(0r)is a left (right) zero element in A
定理:如果0l,0r分别为左右零元,0l=0r=0
proof:0r= 0l * 0r=0r=0
推论:零元是唯一的
proof:let 0’ be anothor zero element , 0’= 0’ * 0 = 0
定理:设o为S上的二元运算,e和0分别为o运算的单位元和零元,如果S至少有两个元素,则e≠0
proof: let e=0,for any x belongs to S
we have x = x o e = x o 0 = 0
Contradiction
So e ≠ 0
逆元-inverse element(有点儿像乘法里的互为倒数,运算结果为单位元1)
* is a binary operation over A, 1∈A is the identity element,for any x belongs to A,
If there is y ∈ A, such that x*y=e,
then x is the left inverse element of y, y is the right inverse element of x
if there is y ∈A,such that x * y=e,y * x=e,
then y is the inverse element of x,denoted as y=x-1(上标)
定理:o为S上可结合的二元运算,e为该运算的单位元,对于x属于S,如果存在左逆元yl和右逆元yr,则有yl=yr=y
proof: yl o x = e ,x o yr = e
yl o e = yl o (x o yr) = (yl o x) o yr = e o yr
yl = yr
推论:逆元是唯一的
proof:let y,z are different inverse elements of x, then
y = y * e = y * (x * z) = (y * x) * z = e * z = z
代数系统-algebraic system
定义
非空集合S和S上k个一元或二元运算组成的系统称作一个代数系统
运算个数相同、对应运算元数相同,代数常数的个数相同——具有相同的构成成分,同类型的代数系统same type(运算性质不一定相同)
子代数系统-sub-algebraic system
同类型,对代数系统中的所有运算封闭
最大和最小的子代数称为平凡的子代数(最大的子代数是他本身)
S的真子集构成的子代数称为真子代数
积代数-product algebra
suppose V1= <A,o> and V2=<B,*> are two algebraic systems of the same type
V=<A×B, ·>, · is defined as
<a1,b1> ·<a2,b2>=<a1oa2, b1*b2>
V是V1V2的积代数,V1V2是V的因子代数
定理:如果V1V2可交换、结合、幂等,则V可交换、结合、幂等
o * 的单位元、零元也是 · 的单位元、零元
x y分别为o * 的可逆元素,则<x,y>是 · 的可逆元素,其逆元为<x-1,y-1>(上标)
同态与同构-homomorphism&isomorphism
在双射函数的作用下,代数系统V1可以转换成V2,则他们是同构的
V1=<A,o> V2=<B,*>同类型,f:A->B,且任意x,y属于A,有f(x o y) = f(x) * f(y),则称f是V1到V2的同态映射,简称为同态
f是单射的->单同态 injective homomorphism(每一个y都有唯一的x与之对应)
f是满射的->满同态(V2是V1的同态像)surjective homomorphism(值域全覆盖)
f是双射的->同构 isomorphism
群-group
定义
半群-semi-group
满足结合律 的二元运算 构成的代数系统
幺半群-monoid(独异点)
有单位元(identity element)的半群
群同态(同构)-homomorphism(isomorphism)
Homomorphism: <G, * > and <G’, ⊙> are two semi-groups, g:G->G’ is a homomorphism from G to G’ if g(a * b)=g(a)⊙g(b) for any a,b in G
群-group
有逆元(inverse element)的幺半群
有限群-finite group
G是有穷集
无限群-infinite group
G是无穷集
阶-order
群的基数(cardinality)(有穷集集合中元素的个数)
平凡群-trivial group
只有一个元素的群
阿贝尔群(交换群)-commutative group
群中的二元运算是可交换的
群中的幂运算-power
a^0 = e
a^n=a^(n-1)a, n>0
a^n=(a^(-1))^m, n<0,m=-n
群中元素的阶-order of an element
使a^k=e成立的最小正整数k称为a的阶(或者周期)
| 记作 | a | = k,称a为k阶元,若不存在这样的正整数则称a为无限阶元 |
子群-subgroup
G是群,H是G的非空子集,如果H关于G中的运算构成群,则称H是G的子群,H≤G,H为G的真子集时,为真子群
G和{e}均为G的子群,称为平凡子群
判定定理
G为群,H是G的非空子集
- 任意a,b∈H,有ab∈H & H中任意一个元素有逆元
- 任意a,b∈H,有ab^(-1)∈H
- H是有穷集,任意a,b∈H,有ab∈H
陪集-coset
设H是群G的子群,a∈G,Ha(aH)为子群H在G中的右(左)陪集,a为Ha的代表元素(coset representative of Ha)
如果对于任意a∈G,都有aH=Ha,则称H为G的正规子群(不变子群)normal subgroup
任一个阿贝尔群的子群都是正规的
H在G中的陪集数被称为H在G中的指数,记作[G:H]
循环群-cyclic group
若存在a∈G.G=,则G为循环群,a为生成元(generator of G)
若a为n阶元,则G为n阶循环群
若a为无限阶元,则G为无限循环群
定理
(a^(-1))^(-1)=a
(ab)^(-1)=b^(-1)a^(-1)
a^n a^m=a^(m+n)
(a^n)^m=a^(nm)
(ab)^n=a^nb^n(只适用于可交换群)
群满足消去律(用逆元证)
| G is a group, a belongs to G, | a | =r, for any k |
| ①a^k=e iff k=rm for some m 记作r | k |
| ② | a^-1 | = | a |
H是群G的子群
He=H
任意a∈G,有a∈Ha
任意a,b∈G,有,
a∈Hb <=> ab^(-1)∈H <=> Ha=Hb
任意a,b∈G,有aRb <=> ab^(-1)∈H
则R是G上的等价关系(equivalence relation)[a]R(下标)=Ha
- 推论
- Ha=Hb or Ha∩Hb=空集
∪{Ha a∈G}=G
- 推论
左右陪集的数目相等
**拉格朗日定理:G为有限群 G = H · [G:H]** - 无限循环群只有两个生成元即a和a^(-1)
格和布尔代数-lattice&Boolean algebra
定义
格(基于偏序集,哈斯图)
partially ordered set<L,≼ >(偏序集)such that for any a , b∈L,they have the least upper bound(最小上界)and the greatest lower bound(最大下界)
格(基于代数系统)!重要
<L,*, · > is an algebraic system, where L is a non-empty set. L is a lattice if * and · satisfy associative laws, commutative laws and absorption laws.满足结合律、交换律、吸收律(幂等律可由吸收律证得)
子格-sub-lattice
S是L的非空子集,S关于L中的运算∨和∧仍构成格,则称S为L的子格
(啊啊啊啊啊啊我为什么要学离散,又累又困又饿又恐惧,我想回家!!!)
格同态
<L,∧,∨> and <S,*,· > are lattices, function f:L→S is a lattice homomorphism if, for any a,b∈L
f(a∧b)=f(a)*f(b),f(a ∨ b)=f(a)·f(b)
分配格-distributive lattice
<L, ∧,∨> is a lattice, 任意a,b,c∈L
a ∧ ( b ∨ c )=( a ∧ b ) ∨ ( a ∧ c )
a ∨ ( b ∧ c )=( a ∨ b ) ∧ ( a ∨ c )
易证a∧(b∨c)=(a∧b)∨(a∧c) <=> a∨(b∧c)=(a∨b)∧(a∨c)
五角格&钻石格
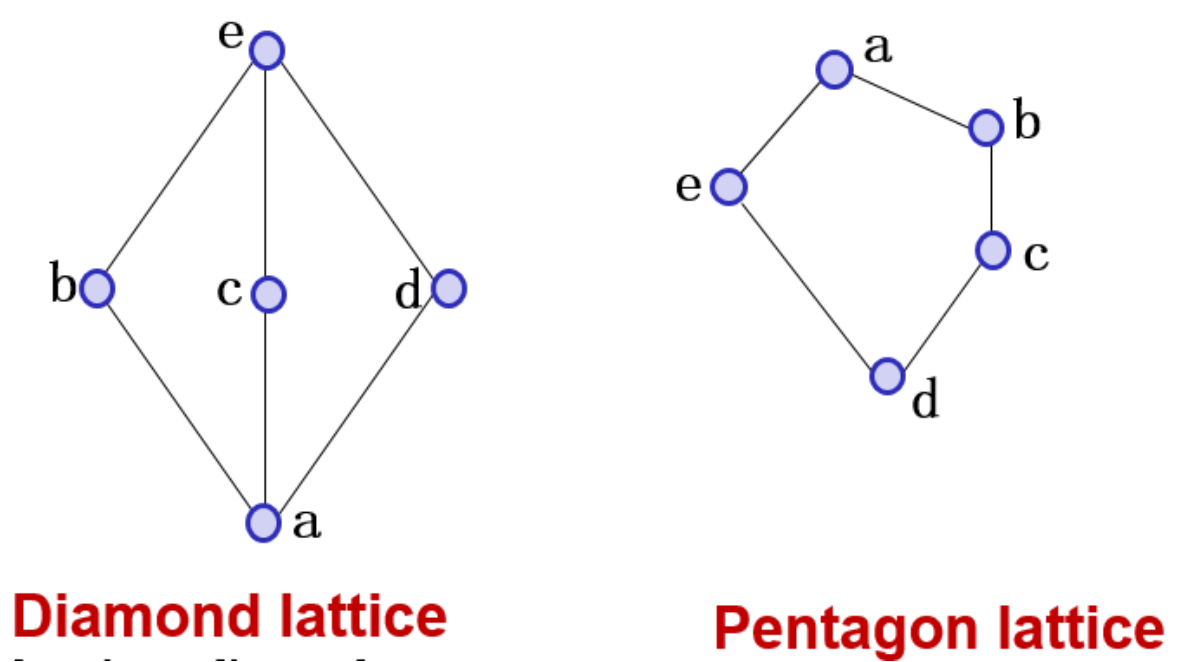
钻石格,五角格
当且仅当L不含与钻石格或五角格同构的子格时,L为分配格
有补格-complemented lattice
有界格-bounded lattice
全上(下)界-Greatest(Least) bound
a∈L,使任意x∈L有x≼a(a≼x),则称a为L的全上(下)界
设L是格,若L存在全上界和全下界,则L为有界格,记作< L, ∧,∨ ,1,0>
/有限格一定是有界格 /
补元-complement element
< L, ∧,∨,0,1> is a bounded lattice, a∈L, if there exists b∈L
a ∧ b = 0,a ∨ b = 1
b是a的补元,记作a’ (a与b互为补元)
有补格
有界格中任一元素都有补元,则该格为有补格
布尔代数(基于格)
有补分配格->布尔格/布尔代数,记作<B,∧,∨,‘,0,1>
#### 布尔代数(基于代数系统)
<B, * , · > 是代数系统, * 和 · 是二元运算,且 * 和 · 满足交换律(commutative laws)、分配律(distributive laws)、同一律(a * 1=a,a · 0=a)(identity laws)、补元律(a · a’=1,a * a‘=0)(complementation laws),则为布尔代数
子布尔代数-sub-boolean algebra
是B的子集,有界,对三个运算封闭
同态
< B,∧,∨,’,0,1 > and
<B‘,+,X,-,α,β > are two Boolean algebra
f is a mapping from B to B‘, satisfying
f(a+b)=f(a)+f(b)
f(a·b)=f(a)Xf(b)
f(a’)=f(a)-
f(0)=α
f(1)=β
原子-atom
a covers b:b≤a and b≠a, there is no other element c,such that b<c and c<a
原子(atom): < B,∧,∨,’,0,1>is a Boolean algebra,if a∈B and a covers 0,then a is an atom of B
定理
格
<L,≤>是格,则∨和∧满足结合律、交换律、幂等律、吸收律
<L,≤>是格,任意a,b∈L,
a ≼ b <=> a ∧ b = a <=> a ∨ b = b
<L,≤>是格,任意a,b,c,d∈L,
a ≼ b and c ≼ d => (a ∨ c)≼(b ∨ d)
a ≼ b and c ≼ d => (a ∧ c)≼(b ∧ d)
<L, * , · > is an algebraic system, then we can construct a partial order ≼, such that for any a,b∈L a · b = a ∨ b, a * b = a ∧ b The idea of the construction:
given lattice <L, * , · >, we can define ≼
a≼b <=> a * b=a <=> a · b=b
given lattice <L, ≼>, we can define * and·
a · b= a∨b, a*b=a∧b
小于5元的格和任何一条链都是分配格
设L为有界分配格,若a∈L,且对a存在补元b,则b是a的唯一补元
布尔代数
布尔代数<B,∧,∨,’,0,1>
a∧b=b∧a,a∨b=b∨a
(a∧b)∧c=a∧(b∧c)
(a∨b)∨c=a∨(b∨c)
a∧a=a,a∨a=a
a∧(a∨b)=a, a∨(a∧b)=a
a∨(b∧c)=(a∨b)∧(a∨c)
a∧(b∨c)=(a∧b)∨(a∧c)
a∨0=a,a∧1=a
a∨1=1,a∧0=0
a∨a’=1,a∧a‘=0
a=a’‘
(a∨b)’=a‘∧b‘
(a∧b)’=a’∨b’
a是布尔代数的原子,任意x∈B,有
x∧a = a / x ∧ a = 0
推出:either a≤x or a≤x‘,but never both (x ∧ a=a <=> a ≤ x x ∧ a=0 <=> a ≤ x’) 由x ∧ a=0证明a ≼ x’: a∧(x∨x’)=a (a∧x) ∨(a∧x’)=a 0∨(a∧x’)=a 即 a∧x’=a 当然 a ≼ x‘ 由a ≼ x’ 证明 x ∧ a=0: a ≼ x‘ 等价于 a∧x’=a, 所以 x ∧ a=x∧a∧x’=0<B,∧,∨,’,0,1> is a finite Boolean algebra,for any non-zero element x∈B,there exists atom a such that x∧a=a( i.e., a≤x)
Proof: If x is an atom,then x∧x=x
Otherwise,since x>0,assume there is a descending chain
x≥a1≥a2≥… ≥ak≥0 Then ak covers 0,so x∧ak=ak
有限布尔代数的表示定理 ! 重要 !
设B是有限布尔代数,A是B的全体原子构成的集合,则B同构于A的幂集代数P(A)
推论:
- 任何布尔代数的基数为2^n
- 任何等势的布尔代数都是同构的
图论
图的基本概念
基础定义
无向图-undirected graph
一个无向图G是一个二元组<V,E>
其中:V是一个非空有穷集,称作顶点集,其元素称作顶点或结点(vertice)
E是无序积V&V的有穷多重子集,称作边集,其元素称作无向边,简称为边(edge)记作:e=(v,w) or e=(w,v)(或用<>)
有向图-directed graph
一个有向图D是一个二元组<V,E>
其中:V是一个非空有穷集,称作顶点集,其元素称作顶点或结点(vertice)
E是笛卡尔积VxV的有穷多重子集,称作边集,其元素称作有向边,简称为边(edge)记作:e=(v,w)(或用<>)
相关概念和规定
无向图和有向图统称为图,有时无向图简称为图,常用G表示无向图,D表示有向图,有时G泛指图,V(G),E(G)分别表示G的顶点集和边集, V(G) , E(G) 分别是G的顶点数和边数 顶点数称作图的阶(order),n个顶点的图称作n阶图
一条边也没有的图称作零图(null graph)n阶零图记作Nn(下标)1阶零图称作平凡图(trivial graph)平凡图只有一个顶点,没有边
如果一条边e的两个端点(endpoint)是u和v,则称e与u(v)关联,若u=v则称e为环(loop)若e1=(u,v); e2=(u,v),则称e1,e2为平行边(multiple edge)
既不含平行边也不含环的图称作简单图
如果u和v是同一条边的两个端点,则称这两个顶点相邻(neighbor/adjacent vertices)
在无向图中,顶点v的邻域(neighborhood):
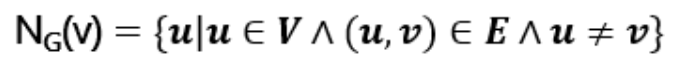
闭邻域(closed neighborhood):
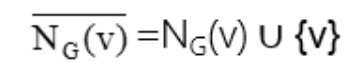
在有向图中,
后继元集(successor set)
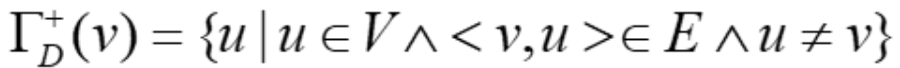
先驱元集(predecessor set)
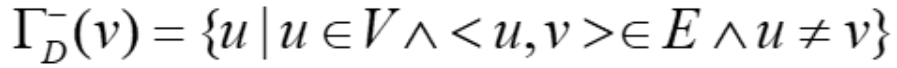
邻域:后继元集和先驱元集的并
闭邻域:同无向图
v作为边的端点的次数称为v的度数(degree),记作d(v)
在有向图中,v作为边的始点的次数称为v的出度,记作d+(v)(+为下标)
v作为边的终点的次数称为v的入度,记作d-(v)(-为下标)

同构
目前只能用矩阵判断两个图是否同构
子图-subgraph

若V’=V,则称为生成子图
完全图-complete graph
每个顶点都与其余顶点相邻的n阶简单图,称作n阶完全图,记作Kn(n≥1)
正则图-regular graph
G为n阶无向简单图,任意v∈V(G),均有d(v)=k,则称G为k-正则图(k-regular)
Kn 是 n-1-正则图
通路-path
G为无向标定图,G中顶点与边的交替序列称作始点到终点的通路
所有边各异——简单通路(simple path)
所有顶点和边都各异——初级通路/路径(primary path)
有重复边——复杂通路
回路-circuit
G为无向标定图,G中顶点与边的交替序列称作始点到终点(始点与终点相同)的回路
所有边各异——简单回路(simple circuit)
所有顶点和边都各异——初级回路/圈(primary circuit)
长度为奇数叫奇圈,偶数叫偶圈
有重复边——复杂回路
基本定理(握手定理)!重要 !
- 在任何无向图中,所有顶点的度数之和等于边数的2倍
- 在任何有向图中,所有顶点的度数之和等于边数的2倍,所有顶点的入度之和等于所有顶点的出度之和,都等于边数
- 推论:在任何图中,奇度(odd)顶点的个数是偶数(even)
- 若对于一个非负整数列存在以V为顶点集,度数列等于该非负整数列的无向图,则称该非负整数列是可图化的,若得到的图是简单图,则称其是可简单图化的。
- 当且仅当非负整数列的和为偶数时,该非负整数列是可图化的
- 设G为任意n阶无向简单图,最大度≤n-1
- 在n阶图G中,若从顶点u到顶点v(u≠v)存在通路,则从u到v存在长度小于等于n-1的通路
- 在n阶图G中,若从顶点u到顶点v(u≠v)存在通路,则从u到v存在长度小于等于n-1的初级通路
- 在n阶图G中,若存在v到自身的回路,则一定存在v到自身长度小于等于n的初级回路
图的连通性
连通图-connected graph
在无向图G中,若u,v之间存在通路,则称u,v是连通的
若无向图G是平凡图或G中任何两个顶点都是连通的,则称G为连通图,否则称之为非连通图
连通分支-connected component
Vi是V关于顶点之间的连通关系的一个等价类,称导出子图G[Vi]为G的一个连通分支,G的连通分支数,记作p(G)
距离:d(u,v)为u,v之间最短的通路的长度
点割集-vertex cut set
An undirected graph G= <V,E>, if there is a set V’⊂V, such that p(G-V’) > p(G), and for any V’’⊂V‘, we have p(G-V’’) = p(G),then V’ is a vertex cut set of G. If V’ only includes one vertex v,then v is cut-vertex割点.
点连通度-vertex connectivity
| κ(G)=min{ | V’ | V’ is a vertex cut set of G} |
规定完全图Kn的点连通度为n-1,非连通图的点连通度为0,若κ(G)≥k,则称为k-连通图
边割集-edge cut set
An undirected graph G= <V,E>。If there eixts E’⊆E such that p(G-E’)>p(G) and for any E’’⊆E’ we have p(G-E’’) =p(G),then E’ is an edge cut set of G. If E’ only includes one edge e,the we call e is a cut edge or bridge割边/桥.
边连通度-edge connectivity
| λ(G)=min{ | E’ | E’is an edge cut set of G} |
非连通图的边连通度为0,λ(G)≥r,则称为r边-连通图
有向图的连通性
若vi到vj之间存在通路,则称vi可达vj(reachable)vi->vj,若同时vj->vi,则称相互可达vi<->vj
长度最短的通路称为短程线,其长度称为距离d<vi,vj>
弱连通图(简称连通图)-weakly connected
有向图D的基图是连通图
单向连通图-unilaterally connected
有向图中任意两点vi,vj,有vi->vj或vj->vi成立
强连通图-strongly connected
任意两点相互可达
/* 强连通图一定是单向连通图,单向连通图一定是弱连通图 */
有向图D是单向连通的,当且仅当D中存在经过所有顶点至少一次的通路
有向图D是强连通的,当且仅当D中存在经过所有顶点至少一次的回路
极大路径-non-extendable path(重要!!!)
Г为一条路径,Г的始点和终点都不与Г以外的顶点相邻,则Г是一条极大路径
/* G is an undirected simple Graph with order n(n≥4) and δ(G)≥3,there is a primary circuit(圈) in G whose length is greater than or equal to 4 */
二部图-bipartite graph
能将V分成V1,V2使G中的每条边的两个端点都是一个属于V1一个属于V2,则称G为二部图(二分图/偶图)称V1和V2为互补顶点子集
完全二部图-complete bipartite graph
| V1中每个顶点均与V2中所有顶点相邻,记作Kr,s, r= | V1 | , s= | V2 |
n阶零图为二部图
定理
任意无向图,有
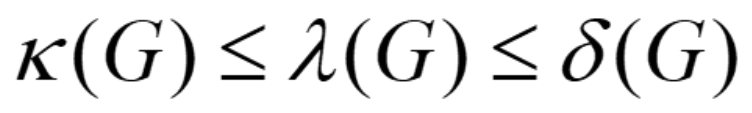
点连通度≤边连通度≤最小度
n阶无向图G是二部图当且仅当G中无奇圈
欧拉图与哈密顿图
欧拉图
欧拉通路&回路-Euler path&cycle
通过图中所有边一次且仅一次行遍所有顶点的通路(回路)
(半)欧拉图-(semi)eulerian graph
具有欧拉回路的图为欧拉图,有欧拉通路而无欧拉回路为半欧拉图
充要条件(会证明!!!)
- 无向图G是欧拉图当且仅当G是连通图且没有奇度顶点
- 无向图G是半欧拉图当且仅当G是连通图且恰有两个奇度顶点
- 有向图D是欧拉图当且仅当强连通且入度等于出度
- 有向图D是半欧拉图当且仅当单向连通且恰有两个奇度顶点,其中一个顶点的入度比出度大1,另一个顶点的出度比入度大1,而其余顶点的入度等于出度
fleury 算法求欧拉回路
- For any v0∈V(G), set P0=v0;
- Suppose Pi=v0e1v1e2…eivi is a path visited, select ei+1 from E(G)-{e1,e2…ei}: a) ei+1 is associated with vi and it should not be the bridge of G-{e1,e2,…,ei} unless there are no other choices b) Suppose ei+1 =(vi,vi+1), add ei+1 vi+1 to Pi and get Pi+1 c) i=i+1
- Stop when all edges are visited
哈密顿图
哈密顿通路&回路-Hamiltonian path&cycle
经过图中所有顶点一次且仅一次的通路(回路)
(半)哈密顿图-(semi)Hamiltonian graph
具有哈密顿回路的图为哈密顿图,有哈密顿通路而无哈密顿回路的图为半哈密顿图
必要条件(会证明!!!)
若无向图G<V,E>是哈密顿图,则对于任意的V的子集S,有
p(G-S) ≤ S 若无向图G<V,E>是半哈密顿图,则对于任意的V的子集S,有
p(G-S) ≤ S + 1 设二部图G<V1,V2,E>
若G是哈密顿图, V1 = V2 若G是半哈密顿图, V2 = V1 +1 若 V2 ≥ V1 +2,则G既不是哈密顿图也不是半哈密顿图
充分条件
设G是n阶无向简单图,若对于G中任意不相邻的顶点u,v,均有d(u)+d(v)≥n-1,则G是半哈密顿图
设G是n阶无向简单图,若对于G中任意不相邻的顶点u,v,均有d(u)+d(v)≥n,则G是哈密顿图
最短路径
带权图
所有边的权之和称作通路的长度
长度最短为最短路径,长度称为距离d
d(u,u)=0,当u和v不可达时,d(u,v)=+∞
dijkstra标号法
用于求最短路径
只用于正权图
树-tree
连通无回路的无向图称作无向树,简称树
每个连通分支都是树的无向图称作森林
平凡图称作平凡树
悬挂顶点称作树叶
度数大于等于2的顶点称作分支点
生成树-spanning tree
如果无向图G的生成子图T是树,则称T是G的生成树
设T是G的生成树,G的在T中的边称作T的树枝,不在T中的边称作T的弦,称T所有弦的导出子图为T的余树
求最小生成树
kruskal算法(加边)
prim算法(加点)
根树-rooted tree
若有向图的基图是无向树,则称这个有向图为有向树
一个顶点的入度为0,其余顶点的入度为1的有向树称作根树
入度为0的顶点称作树根

最优二叉树-optimal binary tree
Huffman 算法
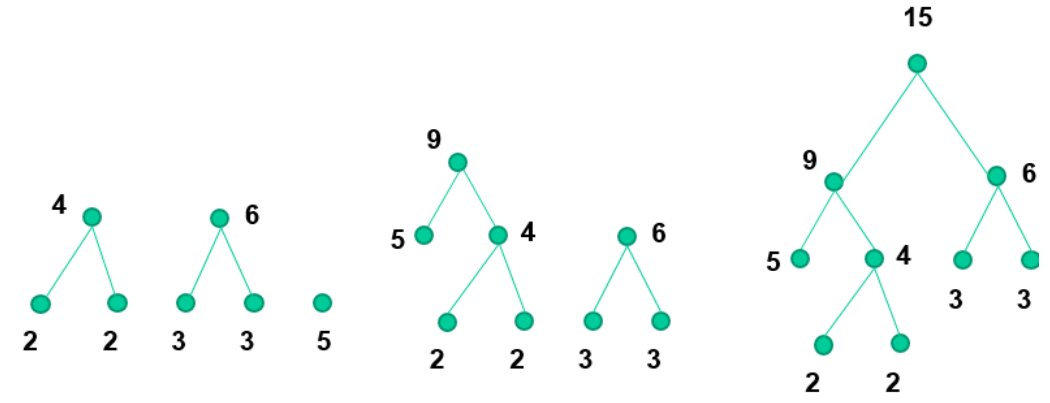
每次选两个最小的入度为0的点
最佳前缀码
性质
- 下列命题相互等价,G=<V,E>是n阶m条边的无向图
- G是树
- G中任意两个顶点之间存在唯一的路径
- G中无回路且m=n-1
- G是连通的且m=n-1
- G是连通的且任何边均为桥
- G中没有回路,但在任何两个不同的顶点之间加一条新边后所得的图中有唯一的一个含新边的圈
- n阶非平凡的无向树,至少有两片树叶
平面图-planar graph
定义
如果能将无向图G画在平面上使得除顶点处外无边相交,则称G为可平面图,简称平面图。
画出的无边相交的图称作G的平面嵌入。
无平面嵌入的图称作非平面图
给定平面图G的平面嵌入,G的边将平面划分成若干个区域,每个区域都称作G的一个面,其中有一个面的面积无限,称作无限面或外部面,其余面的面积有限,称作有限面或内部面,包围每个面的所有边组成的回路组称作该面的边界,边界的长度称作该面的次数记作deg(R)
极大平面图
G为简单平面图,若在G的任意两个不相邻的顶点之间加一条边,所得图为非平面图,则称G为极大平面图
同胚
若两个图同构,或通过反复插入、消去2度顶点后同构,则称两个图同胚
定理
平面图的子图都是平面图,非平面图的母图都是非平面图
Kn(n≤4)和K2,n(n≥1)的所有子图都是平面图
Kn(n≥5)和Ks,t(s,t≥3)都是非平面图
- 设G是平面图,则在G中加平行边或环后所得的图还是平面图
- 平面图所有面的次数之和等于边数的两倍
- 极大平面图是连通的,并且当阶数大于等于3时没有割点和桥
- 设G时n(n≥3)阶简单连通的平面图,G为极大平面图当且仅当G的每个面的次数均为3
欧拉公式
设连通平面图G的顶点数、边数和面数分别为n,m和r,则有n-m+r=2
推广
对于有k(k≥2)个连通分支的平面图G,有n-m+r=k+1
相关定理
- 设G是连通的平面图,且每个面的次数至少为l(l≥3),则G的边数m与顶点数n有
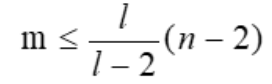
设平面图G有k(k≥2)个连通分支,各面的次数至少为l(l≥3),则G的边数m与顶点数n有

设G是n阶m条边的极大平面图,则(n≥3)
m=3n-6
设G是n阶m条边的简单平面图,则(n≥3)
m≤3n-6
设G是简单平面图,则G的最小度δ(G)≤5
平面图的充要条件
kuratowski定理1
G是平面图,当且仅当G中既不含与K5同胚的子图,也不含与K3,3同胚的子图
kuratowski定理2
G是平面图,当且仅当G中既没有可以收缩到K5的子图,也没有可以收缩到K3,3的子图
对偶图
在G的每一个面Ri中放置一个顶点vi* ,设e为G的一条边,若e在G的面Ri与Rj的公共边界上,则做边e* =(vi* ,vj* )与e相交,且不与其他任何边相交,若e为G中的桥且在面Ri的边界上,则作以vi* 为边界的环e* ,称G* 为G的对偶图
性质
- G* 是平面图,而且是平面嵌入
- G* 是连通图
定理
设G是连通平面图G的对偶图,n,m,r和n,m,r分别为G*和G的顶点数,边数和面数,则
n*=r
m* =m
r* =n
设G* 的顶点v* 位于G的面Ri中,
则dG* (vi* )=deg(Ri)
设G是具有k(k≥2)个连通分支的平面图G的对偶图,n,m,r和n,m,r分别为G*和G的顶点数,边数和面数,则
n* =r
m* =m
r* =n-k+1
设G* 的顶点vi* 位于G的面Ri中,
则dG* (vi* )=deg(Ri)
自对偶图
与对偶图同构
