信息检索基础概述
Published:
本文将根据 elastic search 的原理,按照信息检索的一般流程对信息检索进行简要的介绍,旨在从较高层面了解大致流程,不会深入细节和具体实现。
数据采集
这一步是为后续的检索提供用于搜索的语料数据,并做预先的处理。
使用爬虫相关技术收集所需数据
数据清洗
- 去除空数据
- 去除重复数据
- 去除明显错误的数据
构建停词表、叙词表
停词表
无意义的标点、符号、字词等
叙词表
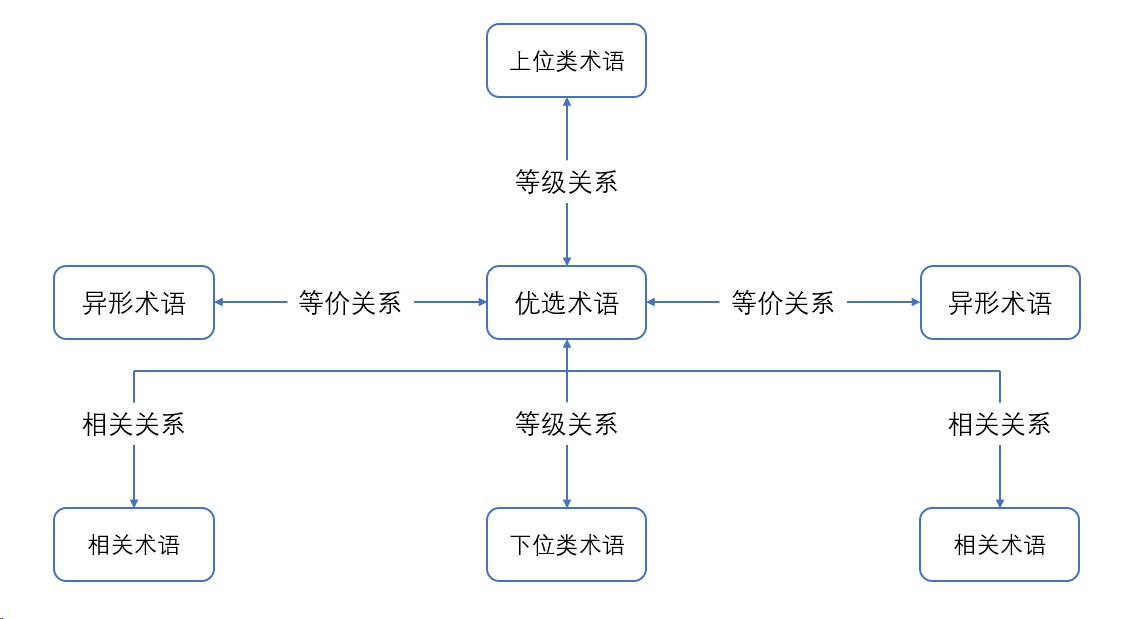
主要为同义词表
中文分词
由于中文没有自然的分隔符,相较于英文分词,难度更大,更易产生歧义,常使用字典、隐马尔可夫模型、机器学习等方法,不是本文的重点,故不做具体介绍。
建立倒排索引
倒排索引是实现高效索引的关键,经过分词处理后得到的项作为 term 项,每项对应其所在文档编号的 postings list 倒排索引,如下图(例子中为方便举例,直接划分至字,没有进行分词)
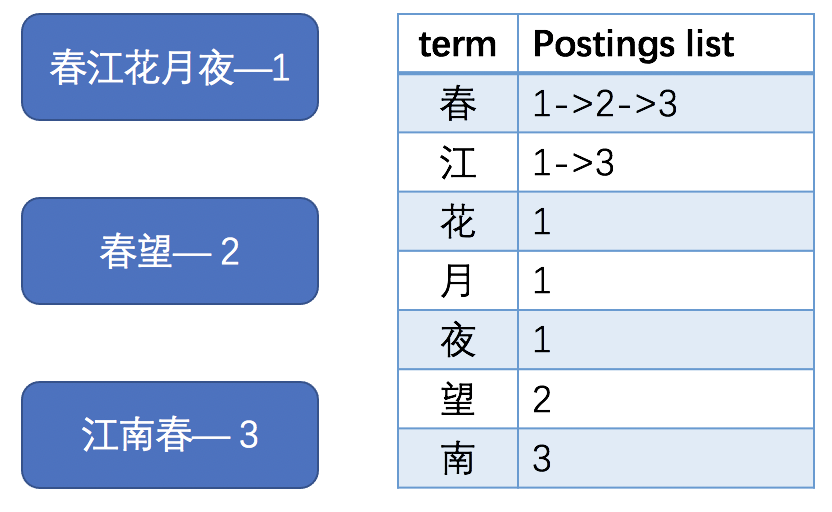
同时,为了更高效地对 term 项进行检索,elastic search 采取了FST的结构,FST(Finite State Transducer)类似于 TRIE 树的结构,各 term 项可共用相同的前缀或后缀,但不同的 term 项到达结尾计算到的数值不同。
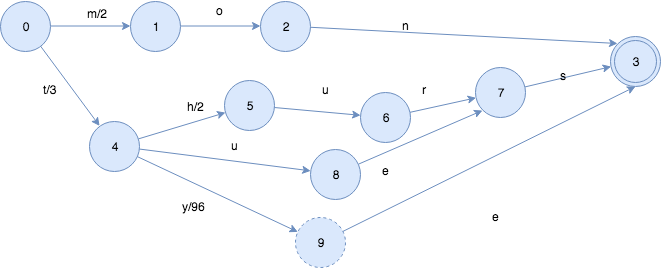
下图即为完整的 term dict index 词典索引树、term dict 词典、invert index 倒排索引的大致结构。
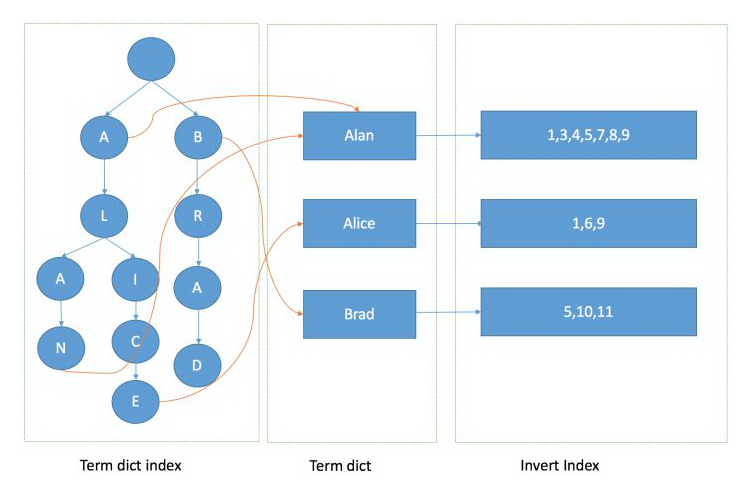
优化
对于大规模的信息检索,其数据量往往会达到十分庞大的程度,此时能否高效地存取也是影响检索效率的一个重要因素。针对这一问题,elastic search 采取了下列两种方法进行磁盘压缩存储与缓存查询优化。
Frame of Reference
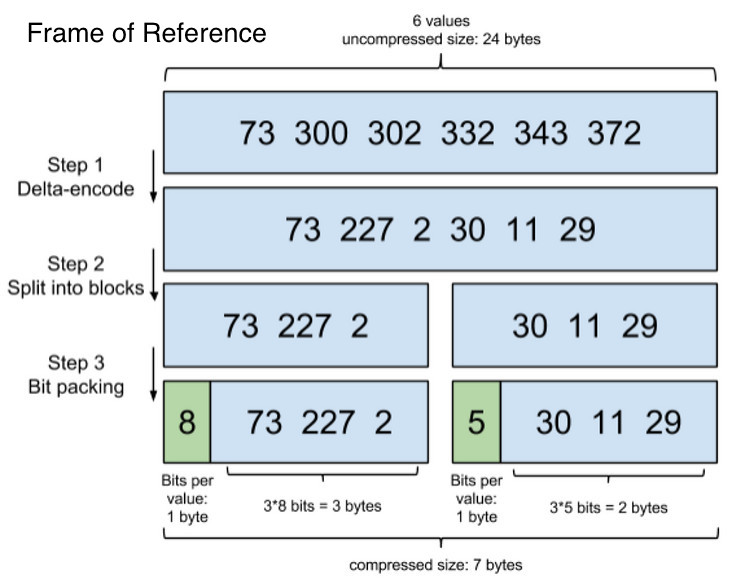
此方法流程如下图,首先将文档列表处理为增量列表,然后将其划分为大小为 256 的块,然后进行按需分配,这里每块的第一位将记录块内各项所需的位数,之后各项根据最大项所需的位数存储。这样,就实现了压缩存储的倒排索引。
Roaring Bitmaps
上述的 Frame of Reference 方法很好地解决了倒排索引在磁盘中的存储问题,而对于分块存储的倒排索引来说,需要频繁的求并集,面对多条件查询时还需要进行交集操作,对于快速的交并集操作,elastic search 采用了 Roaring Bitmaps 的方法,在缓存中进行压缩。
在介绍 Roaring Bitmaps 之前,我们先来介绍两种压缩方法:
数组
也就是直接使用原始的文档 ID,进行数组操作,但这种方法显然不适合 elastic search 每次计算的数据量。
Bitmap
Bitmap 是一个常用的数据结构,我们通过一个例子来了解一下他的结构,我们现在有[2,3,5]和[1,3,4,5]两个数组,将其使用 Bitmap 来表示即为[0,0,1,1,0,1]和[0,1,0,1,1,1],也就是原数组中的值所对应的 Bitmap 中相应脚标的值为 1,其余为 0。这样如果我们要对两个数组取交集,那么我们就对他们的 Bitmap 做与运算,取并集,就做或运算。
我们看到 Bitmap 比较好地完成了对数组的压缩,无论原文档列表中各项的大小是多少,在 bitmap 中都只需要用一位的 0 或 1 来表示。事实上,相当长一段时间内,elastic search 都是采用这种方法的,直到 lucene5 开始使用 Roaring Bitmaps,这主要是为了解决 Bitmap 在稀疏情况下造成的空间浪费。
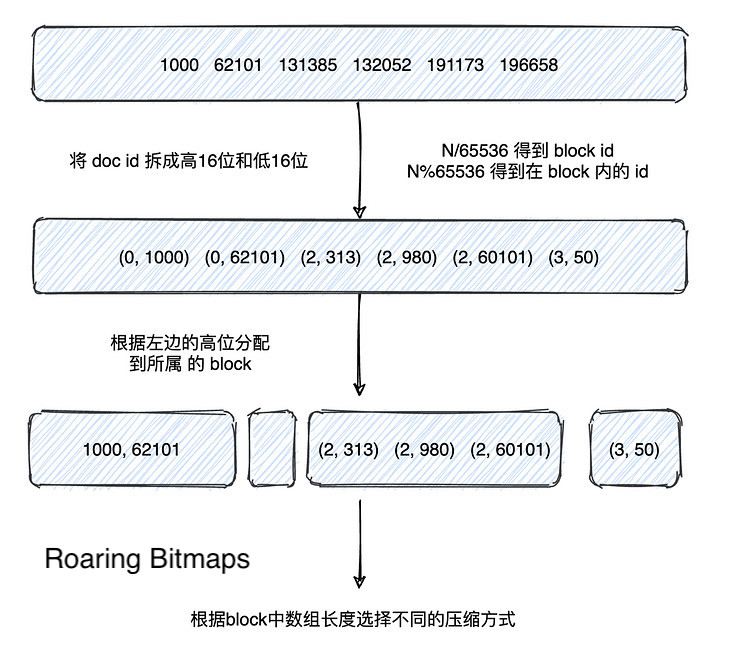
对于文档列表,使用 N/65536 得到该文档对应的块号,然后使用 N%65536 得到该文档在块内的 id,接下来根据不同的块号将文档分配的所属的块,最后根据块内文档数进行数组或位图的选择,这里的阈值来源于实际数据,当超过 4096 时选用位图,反之选用数组。
相关度计算
上一节中介绍的倒排索引让我们能够快速找到包含检索词的文档,但是当相关文档很多时,如果直接按照存储顺序呈现给用户,往往不会带来比较好的体验,我们需要计算文档与检索词的相关度,将最符合用户检索需求的结果排在靠前的位置。
为了进行相关度的计算,让我们先来了解几个参数
\[词频:tf_{t \in d} = \sqrt{frequency}\] \[逆向文档频率:idf_t = 1 + \log(\frac{numDocs}{docFreq+1})\] \[字段长度归一值:norm_d = \frac{1}{\sqrt{numTerms}}\]其中:
- frequency:词 t 在文档 d 中出现的次数
- numDocs:代表索引中文档数量
- docFreq:代表包含词 t 的文档数
- numTerms:代表所在字段的词数
由此,相关度计算公式如下:
\[score_{q,d} = coord_{(q,d)} * \sum_{t \in q}{tf_{t \in d} * idf_{t}^2 * Boost * norm_{(t,d)}}\]其中:
- \[coord_{(q,d)}:\frac{文档中包含的查询词数}{查询词总数} Boost:设定参数\]
排序
上一节中,我们已经根据词频等数据计算得到了各篇文档的相关度,接下来需要对其进行排序,大量数据表明,按相关度降序排序后的前 20 条结果可以满足大多数用户的一般查询需求。因此,通常情况下我们不需要将全部查询结果返回给用户,只需要将前 K 个最符合查询需求的记录返回给用户即可,这里的 K 通常为 20。
这也就是十分常见的topK 问题,最基础的解法是将全部数据进行排序,然后取其前 K 个,但这种方法复杂度较高,在数据量比较大的时候并不适用。
一般来讲,我们采用最大堆/最小堆的方法,我们维护一个有前 k 个最大值构成的小顶堆,每拿到一个数据,就将其与堆顶数据比较,如果大于堆顶数据,则将堆顶数据删除,将新数据插入,反之则不做处理,这样当对全部数据遍历一遍后,堆中数据即为前 k 个最大值。若使用大顶堆,则开始遍历前对全部数据取反即可。
还可以使用快排的思想来解决 topK 问题,但实现过程较堆的过程相对复杂,故本文不做介绍,感兴趣的朋友可以自行探索。
