Xinrui Zhang(张心睿)

Xinrui Zhang(张心睿)

Ph.D. student, School of Computer Science and Engineering，focusing on causal inference, graph neural network.

基于稀疏注意力机制的多智能体强化学习框架

7 minute read

Published:

本文所介绍的基于稀疏注意力机制的多智能体强化学习框架，来自于发表在KDD 2022上的论文”S2RL: Do We Really Need to Perceive All States in Deep Multi-Agent Reinforcement Learning?”，作者来自于浙江大学和华为诺亚方舟实验室。

S2RL: Do We Really Need to Perceive All States in Deep Multi-Agent Reinforcement Learning?

多智能体强化学习背景

多智能体强化学习是指同时存在多个智能体（agents）的强化学习问题。在这种情况下，每个智能体都需要通过与环境的交互来学习如何做出最佳决策，以达到其个体或集体的奖励最大化目标。

基本概念

在单智能体强化学习中，只有一个智能体与环境进行交互学习，智能体需要通过观察环境的状态，选择合适的动作来最大化自己的奖励。马尔科夫决策过程是描述强化学习问题的形式化框架。它由状态、动作、转移概率、奖励函数等组成。马尔科夫性质指的是当前状态包含了过去的所有信息，未来状态的转移只依赖于当前状态和采取的动作，与过去的状态无关。这个过程可以用以下概念进行描述：

  • 状态（State）： 描述环境当前的特征或情况。
  • 动作（Action）： 智能体可以采取的行动。
  • 奖励（Reward）： 用于评估智能体行为的反馈信号，目标是最大化总体奖励。
  • 策略（Policy）： 从状态到动作的映射，决定智能体在给定状态下应该采取什么动作。
  • 值函数（Value Function）： 衡量智能体在给定状态下的长期回报或价值。

与单智能体强化学习相比，多智能体强化学习引入了多个智能体的交互和协作。它们同时存在于同一个环境中，并且智能体之间的行为会影响彼此的奖励，这将单智能体强化学习的马尔科夫决策过程扩展至马尔科夫博弈过程，也就是描述多个智能体相互作用和决策的扩展形式的马尔科夫决策过程。在马尔科夫博弈中，每个智能体的决策都会影响其他智能体的奖励或状态转移概率。与单智能体的MDP不同，马尔科夫博弈需要考虑智能体之间的相互作用和冲突。马尔科夫博弈的目标是找到一组策略，使得每个智能体在其他智能体采用最优策略的情况下，无法通过改变自身策略来获得更高的奖励或效用，这就是纳什均衡。纳什均衡是博弈论中的一个重要概念，描述了多个智能体在给定策略下的稳定状态。在博弈中，每个智能体都选择最优的策略来最大化其自身的收益。纳什均衡指的是当每个智能体都选择了最优策略后，没有任何一个智能体能通过改变自己的策略来进一步提高自己的收益。

由此得到多智能体强化学习的基本概念：

  • 状态（State）： 与单智能体强化学习相同，描述环境当前的特征或情况。
  • 动作（Action）： 与单智能体强化学习相同，智能体可以采取的行动。
  • 奖励（Reward）： 每个智能体都有自己的奖励函数，目标是最大化自身的奖励。智能体的行为选择会影响其他智能体的奖励。
  • 策略（Policy）： 每个智能体都有自己的策略函数，决定在给定状态下应该采取什么动作。智能体的策略需要考虑其他智能体的行为选择来优化自身的奖励。
  • 值函数（Value Function）： 与单智能体强化学习相同，衡量智能体在给定状态下的长期回报或价值。

总的来说，多智能体强化学习与单智能体强化学习的不同之处在于智能体之间存在交互和协作关系。在多智能体强化学习中，每个智能体需要通过观察环境和其他智能体的行为，选择合适的动作以达到自身和整体的最大化奖励目标。这种交互和协作的特点使得多智能体强化学习具有更高的复杂性和挑战性。

多智能体强化学习

根据智能体之间的交互和合作关系，多智能体强化学习可以分为完全合作、完全竞争和混合式关系。

完全竞争关系

多个智能体之间彼此竞争，目标是使自身的奖励最大化，属于双人零和博弈，即智能体获得奖励总和始终为0。每个智能体的决策可以影响其他智能体的奖励，因此智能体需要考虑其他智能体的行为选择来优化自己的策略1。

\[V^ (s)=max_\pi min_{a^-}\sum_{a}Q^ (s,a,a^-)\pi(s,a)\]

对于智能体$i$，它需要考虑在其他智能体$i^-$采取的动作$a^-$令自己$i$回报最差（$min$）的情况下，采取的动作$a$能够获得的最大（$max$）期望回报。基本流程如下：

  • 初始化$V_i(s),Q_i(s,a_i,a^-_i),\pi_i$
  • 对于每一轮博弈：
    1. 第$i$个智能体根据当前状态$s$采用$\epsilon$−贪心策略得到动作$a$并执行；
    2. 得到下一个状态$s^′$ 以及智能体获得的奖励$r_i$，并观测其他智能体$i^−$在状态$s$执行的动作$a^−$；
    3. 更新$Q_i(s,a_i,a^-_i)\xleftarrow{}Q_i(s,a_i,a^-_i)+\alpha[r_i+\gamma V_i(s^{‘}) -Q_i(s,a_i,a^-_i)]$；
    4. 使用线性规划求解$V_i^(s)=max_{\pi_i (s,\cdot)}min_{a_i^-\in A_i}\sum_{a_i\in A_i}Q_i^(s,a_i,a^-_i)\pi_i(s,a_i)$，并更新$V_i(s)$与$\pi_i(s,\cdot)$。

半竞争半合作关系（混合式）

多个智能体既有合作又有竞争的关系。在混合式关系中，智能体之间可能存在相互合作和相互竞争的情况，这要求智能体能够根据具体情况灵活选择合作策略或竞争策略，属于多人一般和博弈2。

\[NashQ_t^i(s^{'})=\pi^1(s^{'})\cdots \pi^n(s^{'})\cdot Q_t^i(s^{'})\]

每个智能体采用普通的Q-learning方法，并且都采取贪心的方式、即最大化各自的Q值时，这样的方法容易收敛到纳什均衡策略。基本流程如下：

  • 初始化$Q_i(s,a_1,\cdots,a_n)=0,\forall a_i\in A_i$；
  • 对于每一轮博弈：
    1. 第$i$个智能体根据当前状态$s$采用$\epsilon$−贪心策略得到动作$a$并执行；
    2. 得到下一个状态$s^′$ 以及智能体$i$观测所有智能体获得的奖励$r_1,\cdots,r_n$，并观测所有智能体在状态$s$执行的动作$a_1,\cdots,a_n$；
    3. 更新$Q_i(s,a_1,\cdots,a_n)\xleftarrow{}Q_i(s,a_1,\cdots,a_n)+\alpha[r_i+\gamma NashQ_i(s^{‘}) -Q_i(s,a_1,\cdots,a_n)]$；
    4. 使用二次规划求解状态$s$处的纳什均衡策略，并更新$NashQ_i(s)$与$\pi_i(s,\cdot)$。

完全合作关系

多个智能体共同合作以实现一个共同的目标，他们的奖励是相同的，个体之间没有竞争。在完全合作的环境中，智能体需要学习如何在不同状态下选择合作动作，以最大化整体奖励。根据智能体完成任务时是否需要通过协作来获得最优回报，可以划分为

不需要协作机制：
  • Team Q-learning3： 假设最优联合动作是唯一的，对于单个智能体，可通过下式求出最优动作。 \(h_i^{x}=argmax_{u_1,\cdots,u_{i-1},u_{i+1},\cdots,u_n}Q^{x,u}\)

  • Distributed Q-learning4： 没有假设协作的条件，但是这种方法只在确定性的场景下有效。每个智能体$i$只通过它自己的动作来维护一个策略$h_i(x)$和一个局部Q函数$Q_i(x,u_i)$，更新方向都是朝着增加$Q_i$的方向进行的。 $$ \begin{aligned}

    Q_{i,k+1}(x_K,u_{i,k})&=max{Q_{i,k}(x_K,u_{i,k}),r_{k+1}+\gamma maxQ_{i,k}(x_{k+1},u_i)} \

    h_{i,k+1}&={

    \begin{array}{lcl}

    u_{i,k} & & if \ max_{u_i}Q_{i,k+1}(x_{k+1},u_i)\neq max_{u_i}Q_{i,k}(x_{k+1},u_i)\

    h_{i,k}(x_k) & & otherwise

    \end{array}

    \end{aligned} $$ 在$Q_{i,0}=0$以及共同奖励为正的情况下，可以证明策略会收敛到最佳联合策略。

隐式协作机制：
  • 联合动作学习（joint action learner，JAL）方法5：}智能体基于观察到的其他智能体的历史动作、对其他智能体的策略进行建模。
  • 频率最大 Q 值（frequency maximum Q-value, FMQ）方法6：}在个体 Q 值的定义中引入个体动作所在的联合动作取得最优回报的频率，从而在学习过程中引导智能体选择能够取得最优回报的联合动作中的自身动作，则所有智能体的最优动作组合被选择的概率也会更高。
  • 基于平均场理论的多智能体强化学习（Mean Field MARL, MFMARL）方法7：}基于平均场理论的建模思想，将所有智能体看作一个“平均场”，个体与其他智能体之间的关系描述为个体和平均场之间的相互影响，从而简化后续分析过程。
显式协作机制：
  • SA-CADRL8（socially aware collision avoidance deep reinforcement learning）：根据该导航任务的具体设定（即机器人处在人流密集的场景中），在策略训练是引入一些人类社会的规则（socially rule），相当于要让机器人的策略学习显式的协作机制，达成机器人与人的行为之间的协作。

多智能体深度强化学习

多智能体深度强化学习是将深度学习技术与多智能体强化学习相结合的一种方法。在值函数的定义或者是策略的定义中引入多智能体的相关因素，并设计相应的网络结构作为值函数模型和策略模型。根据基于策略和基于值函数的划分，多智能体深度强化学习方法可以分为以下两类：

基于策略（Policy-based）：

该方法使用深度神经网络来近似智能体的策略函数。智能体根据观察到的状态选择动作，通过优化策略网络的参数来最大化累积奖励。常见方法有：

  • 多智能体 DDPG 方法9（Multi-Agent Deep Deterministic Policy Gradient, MADDPG）：}联合学习方法，使用集中式评论家（critic）来评估每个智能体的动作价值函数，并使用一个分布式演员（actor）来生成每个智能体的策略。评论家可以访问所有智能体的观测和动作，而演员只能访问自己的观测。
  • 反事实多智能体策略梯度法方法10（Counterfactual Multi-Agent Policy Gradients, COMA）：}联合学习方法，使用集中式评论家来评估每个智能体在给定其他智能体固定策略时采取不同动作所带来的回报差异，并使用一个分布式演员来生成每个智能体的策略。评论家使用反事实基线（将智能体当前的动作和默认的动作进行比较，如果当前动作能够获得的回报高于默认动作，则说明当前动作提供了好的贡献，反之则说明当前动作提供了坏的贡献；默认动作的回报，则通过当前策略的平均效果来提供）来减少方差并避免过拟合。
  • 独立PPO方法11（Independent Proximal Policy Optimization, IPPO）：}独立学习方法，使用近端策略优化（Proximal Policy Optimization, PPO）算法来更新每个智能体的随机策略，并使用一个单独训练出来、固定不变地模拟其他智能体行为的模型。该方法通过减少对其他模型更新频率依赖性，提高了鲁棒性。

基于值函数（Value-based）：

这种方法利用深度神经网络来逼近多智能体系统中每个智能体的动作值函数，如Q函数或V函数。智能体根据当前状态预测最优值然后选择相应动作，通过优化值函数网络的参数来最大化累积奖励，从而指导智能体选择最优的动作，比基于策略的方法更适合大规模的多智能体系统。

  • 值分解网络12（Value Decomposition Networks, VDN）：}使用一个简单的求和操作来组合每个智能体的局部动作值函数，得到一个全局动作值函数，从而降低了计算复杂度和训练难度。
  • QMIX13：}使用一个混合网络来组合每个智能体的局部动作值函数，得到一个单调递增且可微分的全局动作值函数，从而实现对多个合作式智能体进行联合控制。

基于稀疏注意力机制的多智能体强化学习框架

本文所介绍的基于稀疏注意力机制的多智能体强化学习框架，来自于发表在KDD 2022上的论文”S2RL: Do We Really Need to Perceive All States in Deep Multi-Agent Reinforcement Learning?”14，作者来自于浙江大学和华为诺亚方舟实验室。

方法背景

多智能体深度强化学习在很多实际场景中都得到了广泛应用，比如自动驾驶、机器人控制等领域。然而，在实际应用中，每个智能体只能观测到局部信息，并且这些信息通常是不完整和噪声干扰的。因此，在这种情况下，如何让每个智能体都做出正确的决策是一个非常具有挑战性的问题。

针对深度多智能体深度强化学习问题，目前有许多工作致力于提高其性能。在上文介绍的基于值函数的多智能体深度强化学习方法QMIX13中，其将每个智能体的局部观测作为一个整体输入，来影响其执行策略和值函数。然而通常来讲，局部观测可以拆分成多个实体，比如在战争游戏中，某个智能体的局部观测可以拆分成战场环境、敌方位置、队友位置、敌方策略等，这些不同的实体对于智能体作出决策的影响程度也不同，因此在MAAC15中作者引入注意力机制，用于判断不同观测实体对智能体决策的不同重要程度，从而提高智能体决策的有效性、正确性，实现对深度多智能体强化学习方法性能的提升。

然而，由于噪声干扰等，智能体的局部观测往往存在冗余实体，这些冗余实体不仅不能提升智能体决策的效果，反而可能会干扰智能体的决策。例如图中给出的星际争霸II游戏中的例子，对于智能体H3，其当前决策的重要依据是敌方的Z0和Z5，此时战场中他能观测到的其他信息对于他做出移动、攻击等决策没有帮助。

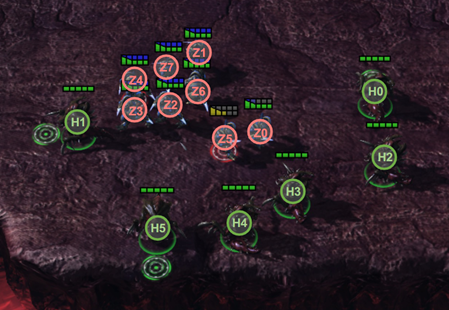
因此本文所介绍的方法提出了基于稀疏注意力机制的深度多智能体强化学习框架S2RL，其使用常规的CTDE（Centralized Training Decentralized Execution）框架，将智能体的局部观测拆分为多个实体后，分别使用自注意力机制和稀疏注意力机制进行注意力权重的计算（使用自注意力机制是因为在初始化时，模型无法判断哪些是冗余实体），自注意力机制的部分与常规自注意力机制计算方式相同，稀疏注意力机制部分可以理解为模型将学习到一个阈值矩阵，用于对各实体的注意力值进行筛选，低于对应阈值的直接设为0。

方法设计

方法定义多智能体强化学习过程为去中心化的部分观察的马尔可夫决策过程如下：

\[M=<\mathcal{J},\mathcal{S},\mathcal{U},P,R,\Omega,G,\gamma>\]
其中，$\mathcal{J}={1,2,\cdots,N}$为智能体的有限集，$s\in\mathcal{S}$表示环境的全局状态，在每个时间步，每个智能体$i\in\mathcal{J}$根据观察函数$G(s,i)$接收一个单独的部分观察$o^i\in\Omega$，并选择一个动作$u^i\in\mathcal{U}$，组成一个联合动作$u$，从而导致根据状态转换函数$P(s^{‘}s,u):\mathcal{S}\times\mathcal{U}\times\mathcal{S}\xleftarrow{}[0,1]$转换到下一状态，所有智能体基于奖励函数$R(s,u):\mathcal{S}\times\mathcal{U}\xleftarrow{}\mathbb{R}$共享同样的全局奖励。由于部分观察的设定，每个智能体有一个动作-观察历史$\tau^i\in T \equiv(\Omega\times\mathcal{U})^*$，并学习其单独的策略$\pi^i(u^i\tau^i)$以获得最大联合回报，联合策略可以导出联合动作值函数$Q_\pi^{tot}(s,u)=\mathbb{E}{s{0:\infty},u_{0:\infty}}[\sum_{t=0}^\infty\gamma^tr_ts_0=s,u_0=u,\pi]$。

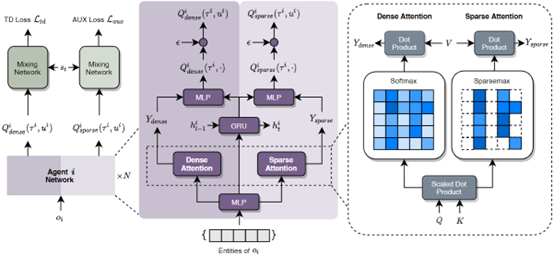
如图为方法模型架构图，其使用CTDE集中式训练分布式执行框架，引入稀疏注意力机制和自注意力机制，具体设计方法如下：

  1. 选择与辨别：
    • 效用网络输入：$O_t^i=[o_t^{i,1},\cdots,o_t^{i,M}]^\top\in\mathbb{R}^{M\times d_E}$；
    • 对所有观察实体做嵌入：$X_t^i={f(o_t^{i,1}),\cdots,f(o_t^{i,M})},i\in\mathcal{J}$；

    • 对每个智能体的观察嵌入特征做自注意力计算： $$ \begin{aligned}

      &Q=XW_Q,K=XW_K,V=XW_V \

      &Attn(Q,K,V)=softmax(\frac{QK^\top}{\sqrt{d_X}})V

      \end{aligned} $$

    • 计算稀疏概率： \(Y_{dense}=Attn(Q,K,V)\in\mathbb{R}^{M\times d_X}\)
    • 使用稀疏概率分布来区分关键实体和不相关实体；
    • 将键值$QK^\top$视作$Z\in\mathbb{R}^M\times M$；
    • 定义矩阵排序器$SortMat(\cdot)$： \(\widetilde{Z}=SortMat(Z)=[SortVec(z_1)^\top,\cdots,SortVec(z_M)^\top]^\top\) 其中，$SortVec(\cdot)$将元素降序排列

    • 计算$n(\widetilde{Z})=[n_1,\cdots,n_M]^\top$;

      其中，$n_m\lesseqqgtr max{n\in[M]1+n\widetilde{Z}{m,n}\ge \sum{k\leq n}\widetilde{Z}_{m,k}}$
    • 定义$c=[c_1,\cdots,c_M]^\top$，其中$c_m=\sum_{k\leq n_m}Z_{m,k}-1$；
    • 定义缩放因子$\mu=[\frac{1}{n_1},\cdots,\frac{1}{n_M}]^\top$；
    • 计算阈值矩阵$\Delta=1_{M\times1}(c\odot\mu)^\top$；

    • 得到稀疏注意力权重矩阵$P=[Z-\Delta]_+$；

      其中,$[\cdot]_+\lesseqqgtr max{0,\cdot}$

    • 计算稀疏注意力$\Delta sAttn(Q,K,V)=PV$；
    • 得到：$Y_{sparse} = sAttn(Q,K,V)\in\mathbb{R}^{M\times d_X}$
  2. 学习： ​
    • 使用GRU编码智能体历史观察和行为；$h_t^i=GRU(X_t^i,h_{t-1}^i)$；

    • 将$Y_{dense}$与$Y_{sparse}$与GRU输出连接： $$ \begin{aligned}

      &Q_{dense}^i=Agent^i(Y_{dense},h_t^i)\

      &Q_{sparse}^i=Agent^i(Y_{sparse},h_t^i)

      \end{aligned} $$

    • 计算主效用损失(TD loss)和辅助效用损失(AUX loss)： $$ \begin{aligned}

      &\mathcal{L}{td}(\theta\pi,\theta_\rho)=\mathbb{E}\mathcal{D}[(r+\gamma \max\limits{u^{‘}}\overline{Q}{dense}^{tot}(s^{‘},u^{‘})-Q{dense}^{tot}(s,u))^2] \

      &\mathcal{L}{aux}(\theta\pi,\theta_\rho)=\mathbb{E}\mathcal{D}[(r+\gamma \max\limits{u^{‘}}\overline{Q}{sparse}^{tot}(s^{‘},u^{‘})-Q{sparse}^{tot}(s,u))^2]

      \end{aligned} $$

    • 每个智能体通过使总损失最小进行训练： \(\mathcal{L}(\theta_\pi,\theta_\rho)=\mathcal{L}_{td}(\theta_\pi,\theta_\rho)+\lambda\mathcal{L}_{aux}(\theta_\pi,\theta_\rho)\)

如图为方法整体流程的伪代码。

方法性能验证

方法在星际争霸II不同难度的6个场景下进行了实验，

  • Easy：

    3s5z

  • Hard：

    3s_vs_ 5z

  • Super-Hard：

    • 6h_vs_ 8z
    • 3s5z_vs_ 3s6z
    • corridor
    • 5s10z

选取七个baseline，S2RL各个场景中均表现出了最佳的效果，对比实验效果如图。

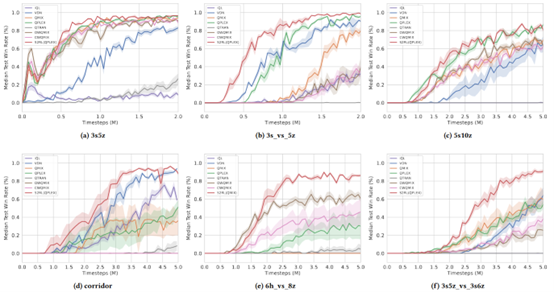
值得注意的是，S2RL可以作为一个通用的模块加入到现有各种基于CTDE框架的深度多智能体强化学习方法中，用于筛选局部观测，在增加了S2RL模块的各种其他方法中，同样体现了S2RL设计对最终效果的提升。

同时，还进行了消融实验，验证了所设计的稀疏注意力机制的效果。

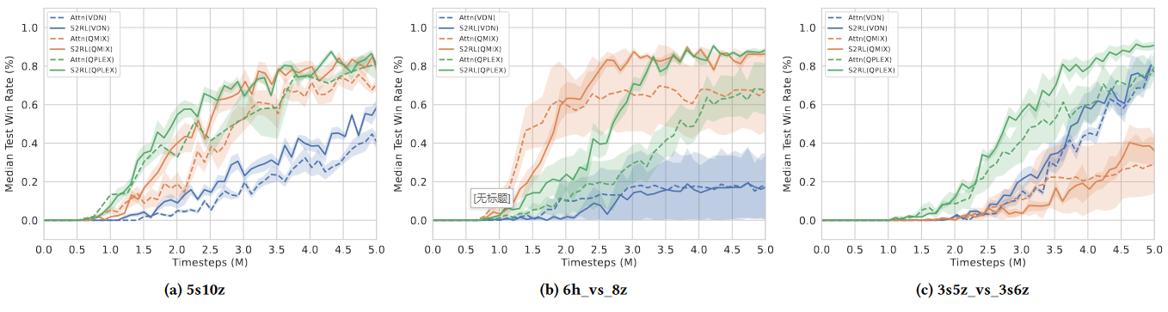
总结

方法总结

本文介绍方法属于基于值函数的多智能体深度强化学习方法，通过引入稀疏注意力机制，实现对各智能体观察到的实体的针对性使用，选择对智能体决策更有效的观察状态，最大化观察状态对智能体决策的帮助，提高多智能体深度强化学习方法性能。

同时，本文介绍的S2RL框架具有即插即用的特性，可作为一个模块，插入到大多数使用集中式训练分布式执行（Centralized Training with Decentralized Execution, CTDE）框架的多智能体深度强化学习方法中，经实验验证，S2RL有效提升了现有CTDE框架多智能体深度强化学习方法的性能。

适用场景

  • 游戏

    • 分布对抗游戏19

      国际象棋、围棋……

    • 实时战略游戏202122

      星际争霸、DOTA……

  • 自动驾驶2324

    无人机、无人车、无人水下航行器编队、调度等

  • 机器人控制2526

    机器人推车、灵巧操作、腿部运动等

  • 交通灯控制27

    自动驾驶车辆与人力驾驶车辆共同行驶

常用基准

基准链接简介
Gridworld28https://github.com/openai/gym离散型动作小球环境
Particle9https://github.com/openai/multiagent-particle-envs连续型动作小球环境
Pommerman29https://github.com/MultiAgentLearning/playground炸弹人环境
Quake III30https://github.com/deepmind/lab雷神之锤III夺旗赛
Google Research Football31https://github.com/google-research/football足球比赛
Multiagent emergence32https://github.com/openai/multi-agent-emergence-environments捉迷藏环境
StarCraft II33https://github.com/oxwhirl/smac星际争霸II对战环境
CARLAhttps://carlachallenge.org/车辆自动驾驶环境
MuJoCo34https://github.com/deepmind/mujoco交通仿真引擎

  1. M. L. Littman, “Markov games as a framework for multi-agent reinforcement learning,” in Machine Learning Proceedings 1994, W. W. Cohen and H. Hirsh, Eds. San Francisco (CA): Morgan Kaufmann, 1994, pp. 157–163. doi: 10.1016/B978-1-55860-335-6.50027-1. ↩

  2. J. Hu and M. P. Wellman, “Nash q-learning for general-sum stochastic games,” J. Mach. Learn. Res., vol. 4, no. null, pp. 1039–1069, Dec. 2003. ↩

  3. M. Lauer and M.A. Riedmiller, “An Algorithm for Distributed Reinforcement Learning inCooperative Multi-Agent Systems,” in Proceedings of the SeventeenthInternational Conference on Machine Learning, San Francisco, CA, USA, Jun.2000, pp. 535–542. ↩

  4. M. L. Littman,“Value-function reinforcement learning in Markov games,” Cognitive SystemsResearch, vol. 2, no. 1, pp. 55–66, Apr. 2001, doi: 10.1016/S1389-0417(01)00015-8. ↩

  5. C. Claus and C. Boutilier, “The dynamics of reinforcement learning in cooperative multiagentsystems,” AAAI/IAAI, vol. 1998, no. 746–752, p. 2, 1998. ↩

  6. S. Kapetanakis and D. Kudenko, “Reinforcement learning of coordination in cooperativemulti-agent systems,” AAAI/IAAI, vol. 2002, pp. 326–331, 2002. ↩

  7. Y. Yang, R. Luo,M. Li, M. Zhou, W. Zhang, and J. Wang, “Mean Field Multi-Agent ReinforcementLearning,” in Proceedings of the 35th International Conference on MachineLearning, Jul. 2018, pp. 5571–5580.  ↩

  8. Y. F. Chen, M. Everett, M. Liu, and J. P. How, “Socially aware motion planning with deep reinforcement learning,” in 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Sep. 2017, pp. 1343–1350. doi: 10.1109/IROS.2017.8202312. ↩

  9. R. Lowe, Y. WU,A. Tamar, J. Harb, O. Pieter Abbeel, and I. Mordatch, “Multi-Agent Actor-Critic for Mixed Cooperative-CompetitiveEnvironments,” in Advances in Neural Information Processing Systems, 2017, vol.30. ↩ ↩2

  10. J. Foerster, G.Farquhar, T. Afouras, N. Nardelli, and S. Whiteson, “Counterfactual Multi-Agent Policy Gradients,” Proceedings of theAAAI Conference on Artificial Intelligence, vol. 32, no. 1, Art. no. 1, Apr.2018, doi: 10.1609/aaai.v32i1.11794. ↩

  11. C. S. de Witt etal., “Is Independent Learning All You Need in the StarCraft Multi-AgentChallenge?” arXiv, Nov. 18, 2020. doi: 10.48550/arXiv.2011.09533. ↩

  12. P. Sunehag et al., “Value-Decomposition Networks For Cooperative Multi-AgentLearning Based On Team Reward,” in Proceedings of the 17th InternationalConference on Autonomous Agents and MultiAgent Systems, Richland, SC, Jul. 2018, pp. 2085–2087. ↩ ↩2

  13. T. Rashid, M. Samvelyan, C. Schroeder, G. Farquhar, J. Foerster, and S. Whiteson, “QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning,” in Proceedings ofthe 35th International Conference on Machine Learning, Jul. 2018, pp.4295–4304. ↩ ↩2 ↩3

  14. Luo, Shuang, et al. “S2RL: Do We Really Need to Perceive All States in Deep Multi-Agent Reinforcement Learning?.” Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. 2022. ↩

  15. S. Iqbal and F.Sha, “Actor-Attention-Critic for Multi-Agent Reinforcement Learning,” inProceedings of the 36th International Conference on Machine Learning, May 2019,pp. 2961–2970. ↩

  16. K. Son, D. Kim,W. J. Kang, D. E. Hostallero, and Y. Yi, “QTRAN: Learning to Factorize with Transformation forCooperative Multi-Agent Reinforcement Learning,” in Proceedings of the 36thInternational Conference on Machine Learning, May 2019, pp. 5887–5896. ↩

  17. J. Wang, Z. Ren,T. Liu, Y. Yu, and C. Zhang, “QPLEX: Duplex Dueling Multi-Agent Q-Learning.” arXiv, Oct. 03, 2021. doi: 10.48550/arXiv.2008.01062. ↩

  18. T. Rashid, G.Farquhar, B. Peng, and S. Whiteson, “Weighted QMIX: Expanding Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning,” in Advances inNeural Information Processing Systems, 2020, vol. 33, pp. 10199–10210. ↩ ↩2

  19. D. Silver et al.,“Mastering the game of Go with deep neural networks and tree search,” Nature,vol. 529, no. 7587, Art. no. 7587, Jan. 2016, doi: 10.1038/nature16961. ↩

  20. “OpenAI Five.”[https://openai.com/research/openai-five](https://openai.com/research/openai-five). ↩

  21. O. Vinyals et al., “Grandmaster levelin StarCraft II using multi-agent reinforcement learning,” Nature, vol. 575,no. 7782, Art. no. 7782, Nov. 2019, doi: 10.1038/s41586-019-1724-z. ↩

  22. S. Liu, G. Lever, J. Merel, S. Tunyasuvunakool, N. Heess, and T. Graepel, “EmergentCoordination Through Competition.” arXiv, Feb. 21, 2019. doi: 10.48550/arXiv.1902.07151. ↩

  23. B. R. Kiran et al.,“Deep Reinforcement Learning for Autonomous Driving: A Survey,” IEEETransactions on Intelligent Transportation Systems, vol. 23, no. 6, pp.4909–4926, Jun. 2022, doi: 10.1109/TITS.2021.3054625. ↩

  24. Y. Cao, W. Yu, W. Ren,and G. Chen, “An Overview of Recent Progress in the Study of DistributedMulti-Agent Coordination,” IEEE Transactions on Industrial Informatics, vol. 9,no. 1, pp. 427–438, Feb. 2013, doi: 10.1109/TII.2012.2219061. ↩

  25. T. P. Lillicrap et al., “Continuouscontrol with deep reinforcement learning.” arXiv, Jul. 05, 2019. doi: 10.48550/arXiv.1509.02971. ↩

  26. J. Li et al., “ShapleyCounterfactual Credits for Multi-Agent Reinforcement Learning,” in Proceedingsof the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, NewYork, NY, USA, Aug. 2021, pp. 934–942. doi: 10.1145/3447548.3467420. ↩

  27. C. Wu, A. Kreidieh, E. Vinitsky, and A. M. Bayen, “Emergent Behaviors inMixed-Autonomy Traffic,” in Proceedings of the 1st Annual Conference on RobotLearning, Oct. 2017, pp. 398–407. ↩

  28. G. Brockman et al., “OpenAI Gym.” arXiv, Jun. 05, 2016. ↩

  29. O. Vinyals et al., “Grandmaster levelin StarCraft II using multi-agent reinforcement learning,” Nature, vol. 575,no. 7782, Art. no. 7782, Nov. 2019, doi: 10.1038/s41586-019-1724-z. ↩

  30. C. Beattie et al.,“DeepMind Lab.” arXiv, Dec. 13, 2016. doi:10.48550/arXiv.1612.03801. ↩

  31. K. Kurach et al., “Google ResearchFootball: A Novel Reinforcement Learning Environment.” arXiv, Apr. 14, 2020. doi:10.48550/arXiv.1907.11180. ↩

  32. B. Baker et al.,“Emergent Tool Use From Multi-Agent Autocurricula.” arXiv, Feb. 10, 2020. doi:10.48550/arXiv.1909.07528. ↩

  33. M. Samvelyan et al., “The StarCraftMulti-Agent Challenge.” arXiv, Dec. 09, 2019. doi:10.48550/arXiv.1902.04043. ↩

  34. E. Todorov, T. Erez, and Y. Tassa, “MuJoCo: A physics engine formodel-based control,” in 2012 IEEE/RSJ International Conference on IntelligentRobots and Systems, Oct. 2012, pp. 5026–5033. doi:10.1109/IROS.2012.6386109. ↩

You May Also Enjoy

图因果效应估计

less than 1 minute read

Published:

该论文发表在 AAAI 2022，介绍了近年来图因果效应估计的代表性方法，以及未来研究方向。

近似算法介绍

5 minute read

Published:

《研究生算法设计》课程报告